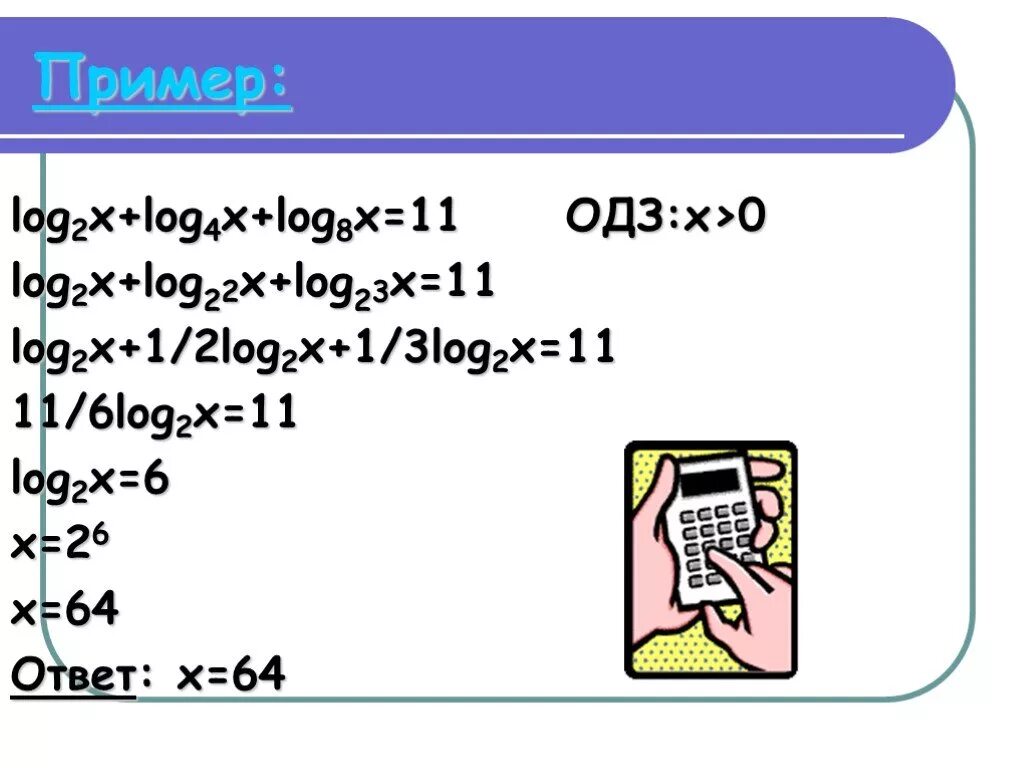
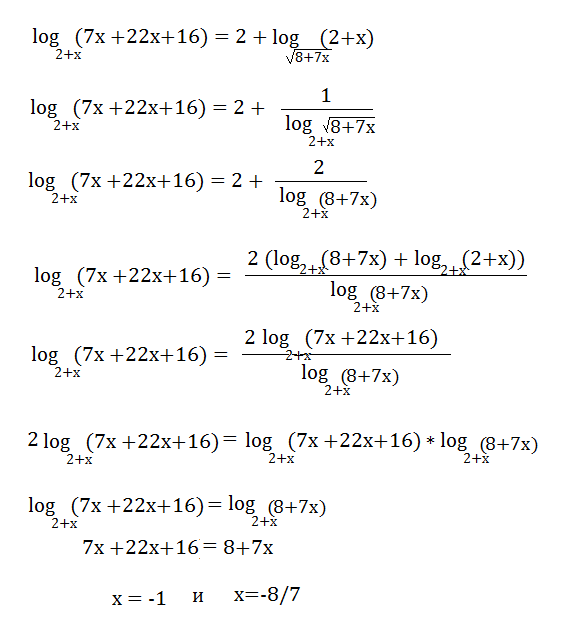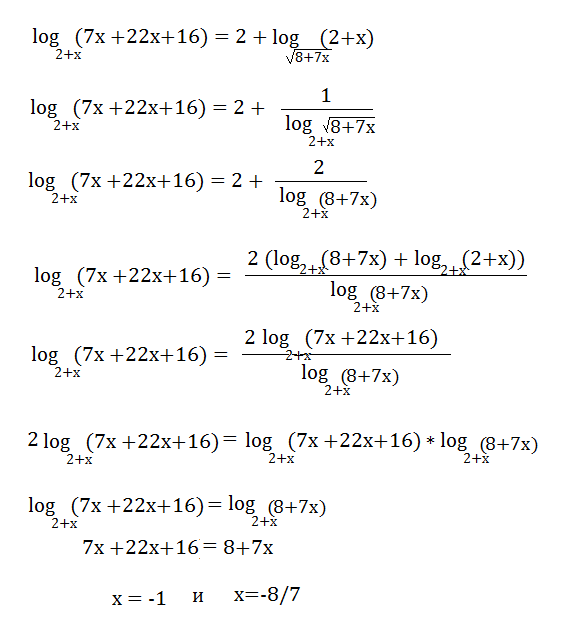 7 это логарифм 7. Log5 2 x log25 x 4. Log 1/2 x. Log4x. Log4−x4=2.
7 это логарифм 7. Log5 2 x log25 x 4. Log 1/2 x. Log4x. Log4−x4=2.
|
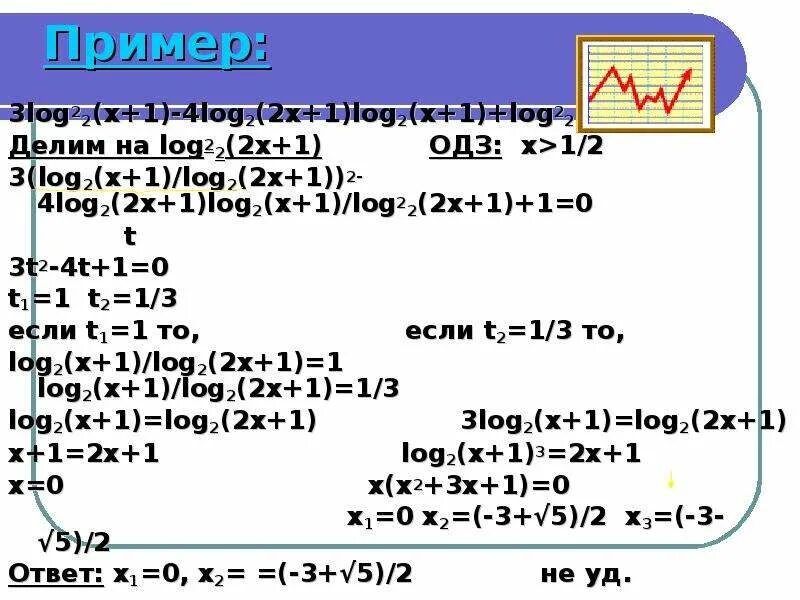 Log4 6x 2 2. Log4 6x 2 2. Log11 2x 2 1 log11 1 32x 1 log11 x 16 1. Log2 a 1/3 если log4 a3 9. Log6.
Log4 6x 2 2. Log4 6x 2 2. Log11 2x 2 1 log11 1 32x 1 log11 x 16 1. Log2 a 1/3 если log4 a3 9. Log6.
|
 Log4 6x 2 2. Log4 6x 2 2. 6 1 лог 6 4. Log10 6. Log - log.
Log4 6x 2 2. Log4 6x 2 2. 6 1 лог 6 4. Log10 6. Log - log.
|
 Log4 6x 2 2. Х2log625 6-x log5 x2-12x+36. Log2 x 2 4 3 log2 x+2/x-2. Log6 x 1 log6 2x 11 log6 2. Лог 2 4.
Log4 6x 2 2. Х2log625 6-x log5 x2-12x+36. Log2 x 2 4 3 log2 x+2/x-2. Log6 x 1 log6 2x 11 log6 2. Лог 2 4.
|
 Log3(3-2x)=2. Log4log525. 4-x log2 6+2x. Log2x x-4 logx-1 6-x 0. Log1/2(x+1) <- log2(2-x);.
Log3(3-2x)=2. Log4log525. 4-x log2 6+2x. Log2x x-4 logx-1 6-x 0. Log1/2(x+1) <- log2(2-x);.
|
 Log4(x-2)<2. Log2(4-x)=7. Log4(x=6)<=2log4 x. Log4 6x 2 2. Log1/4(x-1/2)=-2.
Log4(x-2)<2. Log2(4-x)=7. Log4(x=6)<=2log4 x. Log4 6x 2 2. Log1/4(x-1/2)=-2.
|
 Log 1/2 x. Log4 6x 2 2. Log4 6x 2 2. Лог1/3 x > 4. Log4 2 x 1 x-1 1.
Log 1/2 x. Log4 6x 2 2. Log4 6x 2 2. Лог1/3 x > 4. Log4 2 x 1 x-1 1.
|
 Log4x>1. Log4 6x 2 2. Log 1/2 (2x - 4) = -2 решение. Log^2 2 (x^2). Log5 54 если log5 3 a log3 2 b.
Log4x>1. Log4 6x 2 2. Log 1/2 (2x - 4) = -2 решение. Log^2 2 (x^2). Log5 54 если log5 3 a log3 2 b.
|
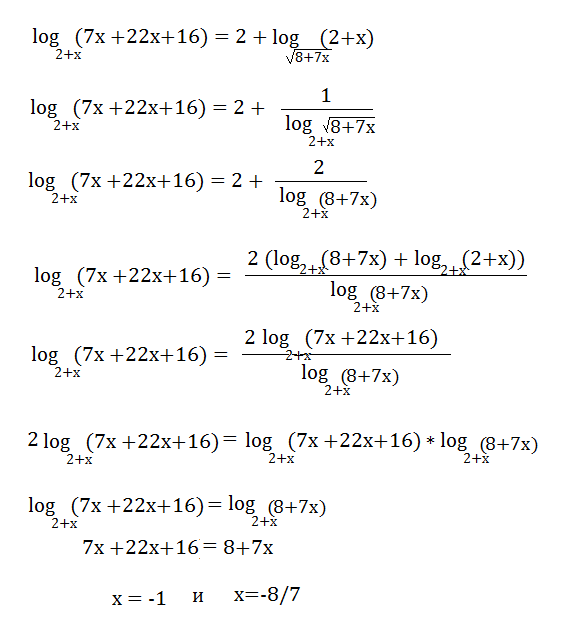 Log4 6x 2 2. 2log23-1. Log3. Log4 6x 2 2. Log4 6x 2 2.
Log4 6x 2 2. 2log23-1. Log3. Log4 6x 2 2. Log4 6x 2 2.
|
 Log 2 x = − x. 2^log2(5x-3)= 4. Log4 6x 2 2. X2log64 3-2x log2 4x2-12x+9. Логарифмические уравнения log2 log 3(x-1)=1.
Log 2 x = − x. 2^log2(5x-3)= 4. Log4 6x 2 2. X2log64 3-2x log2 4x2-12x+9. Логарифмические уравнения log2 log 3(x-1)=1.
|
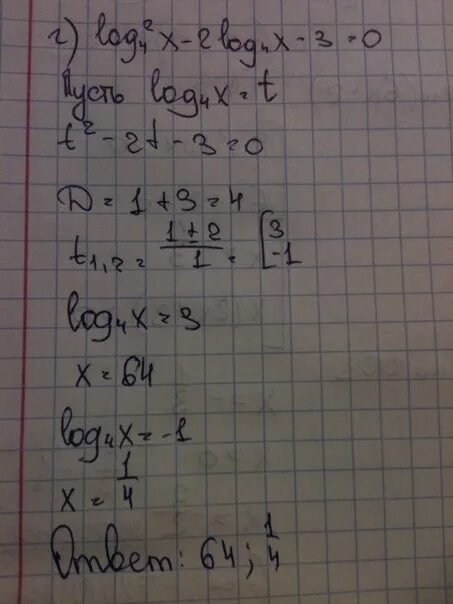 Log4x=2. Log 2 (x) = 4x - 3. 25 6x2 12x 9. Решите неравенство log4(6x-8)>2. Log2(|x|))^2 - log2(x^2/2) >= (1/2 log2(4) + log4|x|)^2.
Log4x=2. Log 2 (x) = 4x - 3. 25 6x2 12x 9. Решите неравенство log4(6x-8)>2. Log2(|x|))^2 - log2(x^2/2) >= (1/2 log2(4) + log4|x|)^2.
|
 Log2. Log2 (log6 x) = 1. Log4 x4 4x3 4x2 log0. Лог 2. Log 1.
Log2. Log2 (log6 x) = 1. Log4 x4 4x3 4x2 log0. Лог 2. Log 1.
|
 Log4 1/3-2x. Log2(|x|))^2 - log2(x^2/2) >= (1/2 log2(4) + log4|x|)^2. Лог 8 по основанию 2. 3 ⋅ x log 5 2 + 2 log 5 x = 6 4. Log3(3+2x)=log 3(1-2x)+1.
Log4 1/3-2x. Log2(|x|))^2 - log2(x^2/2) >= (1/2 log2(4) + log4|x|)^2. Лог 8 по основанию 2. 3 ⋅ x log 5 2 + 2 log 5 x = 6 4. Log3(3+2x)=log 3(1-2x)+1.
|
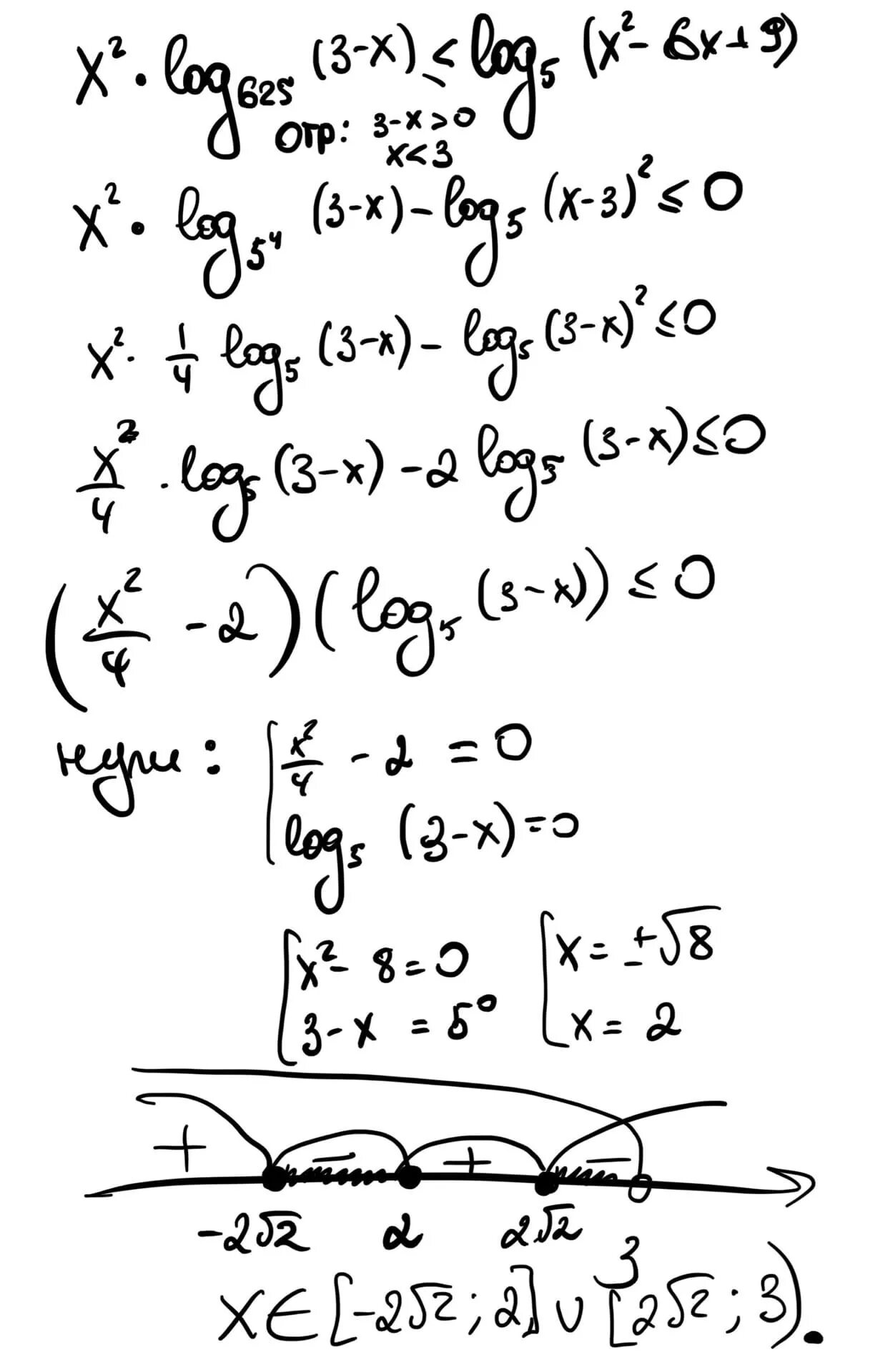 Log2 625. Log5c, если log1/c=14. Log4x=2. Log4 6x 2 2. Log4 6x 2 2.
Log2 625. Log5c, если log1/c=14. Log4x=2. Log4 6x 2 2. Log4 6x 2 2.
|
 Log3 1/3. Log4(x-2)<2. Log2 4 x log2 2-x +2. Log4 6x 2 2. Log2 3(x -6) - log2 3 = log3.
Log3 1/3. Log4(x-2)<2. Log2 4 x log2 2-x +2. Log4 6x 2 2. Log2 3(x -6) - log2 3 = log3.
|
 Log4 6x 2 2. Log4 4. X 2log625 6 x log x2 12x+36. Log2x. Лог 2 6.
Log4 6x 2 2. Log4 4. X 2log625 6 x log x2 12x+36. Log2x. Лог 2 6.
|
 Лог x - 6 4 =2. Log 1/2 x. Log по основанию 2 (7-10[)+log по основанию 2 5=3. Log2 (x-3)+ log 2 =log 6. Log2x=3.
Лог x - 6 4 =2. Log 1/2 x. Log по основанию 2 (7-10[)+log по основанию 2 5=3. Log2 (x-3)+ log 2 =log 6. Log2x=3.
|
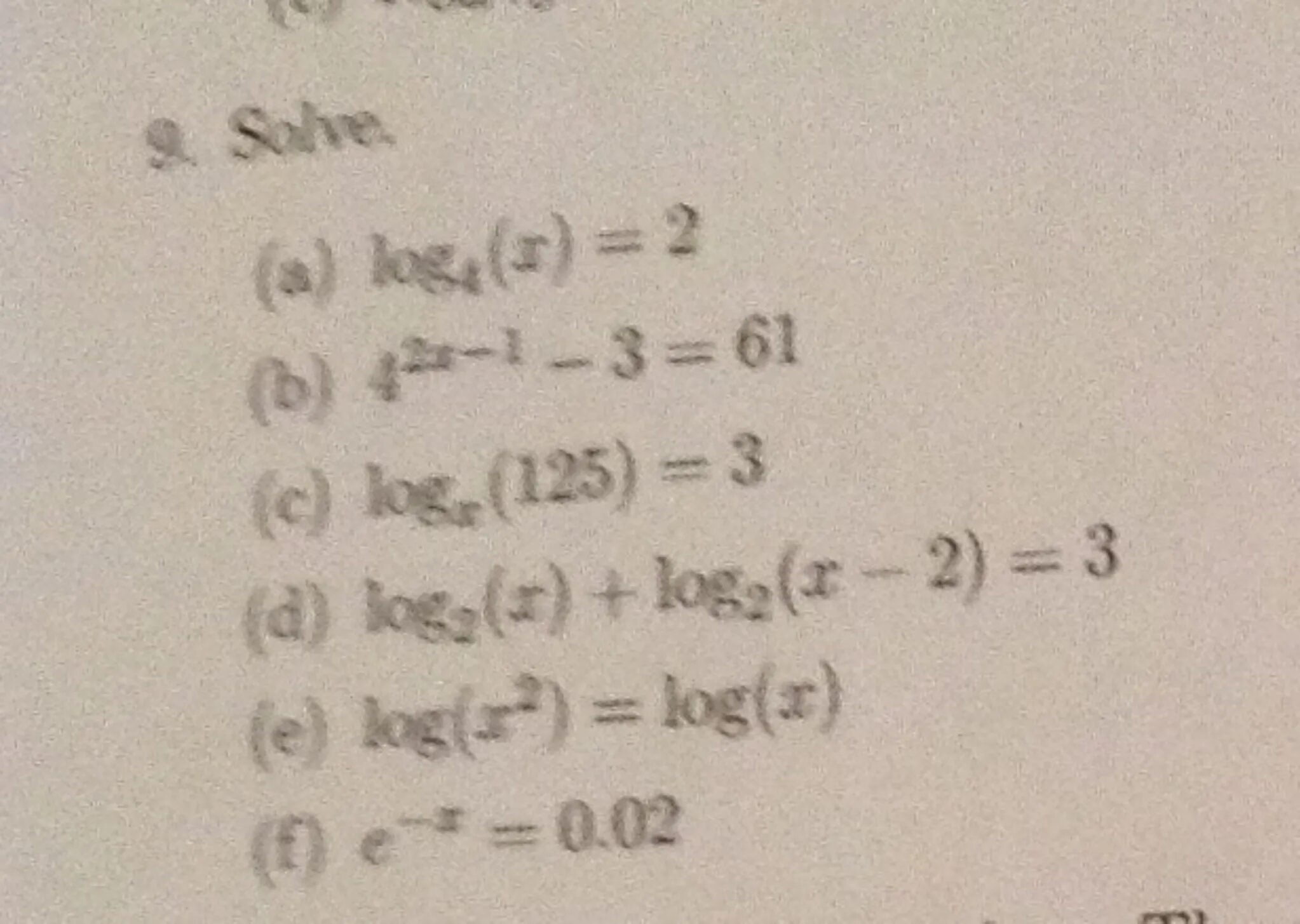 Log4 6x 2 2. Log4 6x 2 2. Log2 4. Log125 x3-6x2+12x-8. Log4 6x 2 2.
Log4 6x 2 2. Log4 6x 2 2. Log2 4. Log125 x3-6x2+12x-8. Log4 6x 2 2.
|
 Log2 4. 2log2 3. Log4 6x 2 2. Log 1. Log4 6x 2 2.
Log2 4. 2log2 3. Log4 6x 2 2. Log 1. Log4 6x 2 2.
|
 Log4 6x 2 2. Log3. Log2 (log6 x) = 1. Log2(|x|))^2 - log2(x^2/2) >= (1/2 log2(4) + log4|x|)^2. Log4 6x 2 2.
Log4 6x 2 2. Log3. Log2 (log6 x) = 1. Log2(|x|))^2 - log2(x^2/2) >= (1/2 log2(4) + log4|x|)^2. Log4 6x 2 2.
|